What is the Dot Product?
The dot product, also known as the scalar product, is a fundamental concept in mathematics and physics. It allows us to measure the relationship between two vectors and provides insights into their angles and lengths. By taking the dot product of two vectors, we can determine if they are orthogonal (perpendicular), parallel, or at an angle to each other. This knowledge is crucial for understanding the geometric properties of vectors and their real-world applications. The dot product operates by multiplying the corresponding components of two vectors and then summing the products. In mathematical notation, the dot product of vectors A and B is denoted as A·B. It can be calculated using the formula:A·B = A₁B₁ + A₂B₂ + A₃B₃ + … + AₙBₙ
Where A₁, B₁, A₂, B₂, etc., represent the components of the vectors A and B. This concept finds practical applications in various fields, including physics, engineering, and computer science. It is used in calculating work done, finding projections, solving problems involving forces and displacements, and much more. Notable variations and related concepts include the cross product, which produces a vector rather than a scalar result, and the inner product, which considers complex numbers instead of just real numbers.- Dot Product – Wikipedia
- Dot Product – Math Is Fun
Understanding the Geometric Properties of Vectors
The dot product plays a crucial role in understanding the geometric properties of vectors. Here are some key insights:- Angle: The dot product allows us to determine the angle between two vectors. When the dot product is positive, the vectors are oriented in a similar direction; when negative, they are oriented in opposite directions. A dot product of zero indicates that the vectors are perpendicular.
- Length: By taking the dot product of a vector with itself, we can find its length or magnitude. The square root of the dot product gives the magnitude of the vector.
- Projection: The dot product can help us find the projection of one vector onto another. It provides a measure of how much of one vector lies in the direction of another.
- Orthogonality: When the dot product of two vectors is zero, they are orthogonal to each other. This property is essential in many applications, including finding orthogonal bases and solving systems of linear equations.
Applications in Computer Graphics
The dot product plays a crucial role in computer graphics, enabling developers to create realistic and visually appealing graphics. Here are some key applications: 1. Illumination and Shading – The dot product is used to determine the intensity of light hitting a surface, which affects how it appears in a 3D environment. By calculating the dot product between the surface normal and the light direction, computer graphics software can simulate realistic lighting and shading effects. 2. Camera Transformations – In computer graphics, the dot product is used to transform 3D objects and scenes into 2D images by projecting them onto a camera’s view plane. This process involves calculating the dot product between the object’s position and the camera’s viewing direction. 3. Collision Detection – When working with 3D models, it is essential to detect whether objects intersect or collide. The dot product can help determine the angle between two vectors, such as the direction of movement and the object’s surface normal, allowing for accurate collision detection in computer graphics simulations and games. 4. Shadows and Reflections – To achieve realistic shadows and reflections in computer-generated scenes, the dot product is used to calculate the angle between the surface normal and the light direction or the viewer’s line of sight. These calculations enable the software to accurately simulate how light interacts with objects in the scene. 5. Texture Mapping – Texture mapping enhances the visual quality of computer-generated images by applying a texture to the surface of an object. The dot product is used to determine the orientation of the surface with respect to the texture, allowing for accurate mapping of the texture onto the object. 6. Anti-aliasing – In computer graphics, anti-aliasing is used to minimize the jagged appearance of lines and edges in images. The dot product is employed to determine the smoothness or sharpness of curves and edges, allowing for the application of anti-aliasing techniques to create smoother and more visually appealing graphics. These applications highlight the versatility and importance of the dot product in computer graphics. By understanding how it operates and integrating it into algorithms and techniques, developers can create stunning visuals and immersive experiences for various applications, including video games, animation, virtual reality, and more. For more information on computer graphics and its applications, click here.Applications in Engineering
Applications in Engineering
In the field of engineering, the dot product plays a crucial role in various applications. Here are some practical examples of how engineers utilize the dot product:- Vector Analysis: Engineers use the dot product to determine the angle between two vectors, which helps in analyzing forces, motion, and structural stability.
- Work and Energy Calculations: By finding the dot product of force and displacement vectors, engineers can calculate the work done on an object or the energy transferred in a system.
- Mechanical Systems: The dot product helps engineers analyze the relationship between forces, displacements, and mechanical work in mechanisms, machines, and structures.
- Electricity and Magnetism: In electrical engineering, the dot product is used to calculate the power consumed or transferred between electrical circuits or magnetic fields.
- Signal Processing: Engineers apply the dot product in analyzing signals, such as audio or video data, to extract useful information or perform transformations.
Challenges and Future Developments
While the dot product is widely used in engineering applications, challenges can arise, such as dealing with large datasets or complex calculations. To address these challenges, engineers are exploring advancements in computational algorithms, parallel processing, and optimization techniques. In the future, with the emergence of new technologies like machine learning and artificial intelligence, the dot product is expected to find novel applications in fields like robotics, autonomous systems, and advanced materials. Its ability to analyze relationships between vectors will continue to be invaluable in solving complex engineering problems.| Application | Industry |
|---|---|
| Vector Analysis | Civil, Mechanical, Aerospace |
| Work and Energy Calculations | Mechanical, Electrical |
| Mechanical Systems | Mechanical, Civil |
| Electricity and Magnetism | Electrical, Electronics |
| Signal Processing | Telecommunications, Media |
Calculating the Dot Product
Calculating the Dot Product
The dot product is a fundamental operation in vector algebra that allows us to determine the relationship between two vectors. By calculating the dot product, we can find the angle between two vectors, determine the length or magnitude of a vector, and even project one vector onto another. To calculate the dot product, we take the product of the corresponding components of the two vectors and then sum them up. This operation can be represented mathematically as:A · B = A1 * B1 + A2 * B2 + … + An * Bn
The dot product is particularly useful in fields such as physics, engineering, and computer science, where it helps in solving problems involving forces, displacements, and projections. Some practical applications of the dot product include:- Calculating work and energy in mechanical systems.
- Determining the angle between vectors in robotics and autonomous systems.
- Analyzing electrical signals using signal processing techniques.
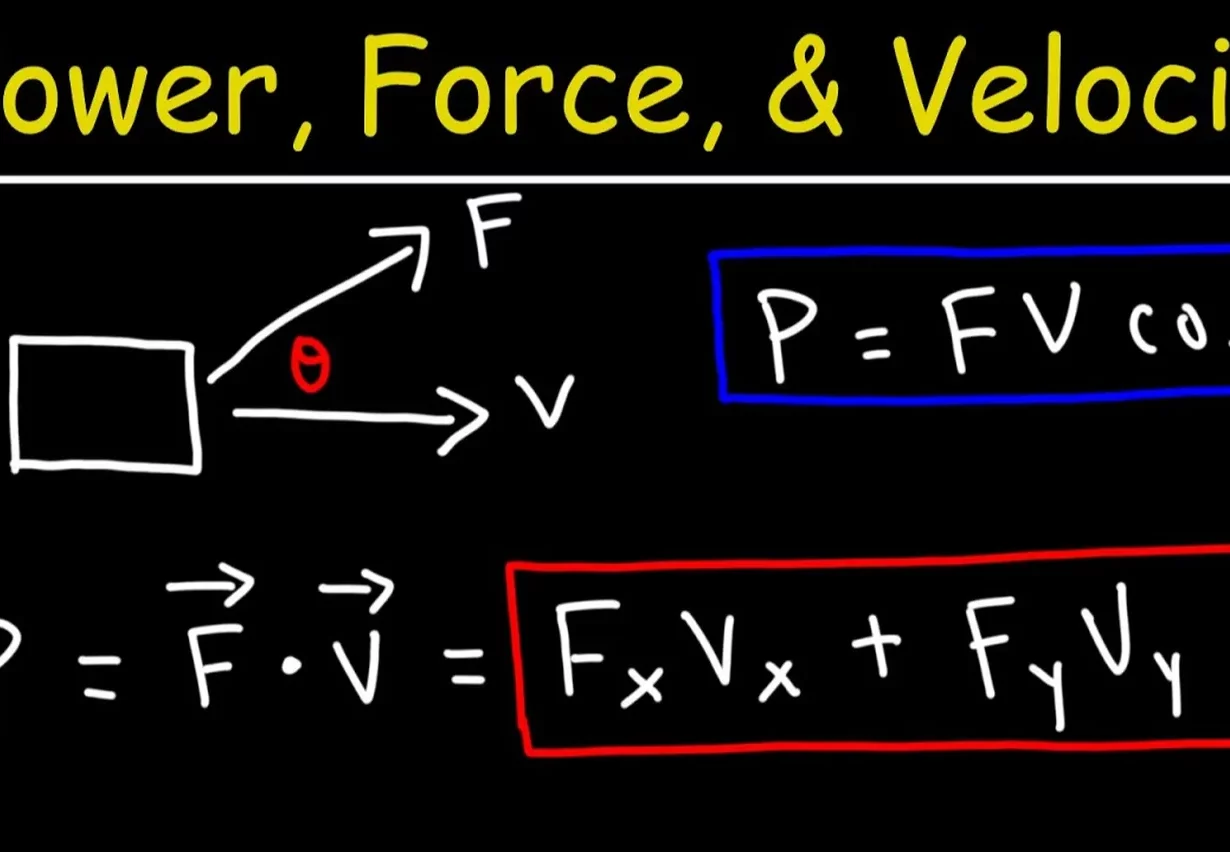
Work Done and Dot Product
The dot product is a fundamental concept in vector algebra that plays a significant role in understanding the physical principles of work. It allows for the calculation of the work done by a force on an object in the direction of the force. The dot product is calculated by taking the magnitude of one vector and multiplying it with the component of the other vector in the same direction. This product represents the scalar projection of one vector onto another. In the context of work, the dot product helps determine the amount of energy transfer that occurs when a force is applied to an object over a certain distance. By finding the dot product between the force vector and the displacement vector, one can calculate the work done on the object. The dot product also has practical applications in fields such as mechanical engineering and physics. It is used to calculate the force exerted on an object given the angle between the force vector and the displacement vector. This information is crucial for designing structures, analyzing forces, and understanding the efficiency of mechanical systems. Another application of the dot product in the context of work is work-energy calculations. By relating the work done on an object to changes in its kinetic and potential energy, one can analyze the conservation of energy in various systems. Challenges that arise when working with the dot product include dealing with complex vectors and understanding the mathematical properties of dot products. Additionally, working with large datasets or performing complex calculations involving multiple dot products can be computationally demanding. In terms of future developments, the dot product is expected to continue playing a crucial role in robotics, autonomous systems, and advanced materials. As technology advances, the dot product will likely be used to analyze and optimize the performance of robotic systems, ensure precise control and navigation, and develop advanced materials with enhanced properties. It’s important to note that the dot product is closely related to other concepts such as the cross product and the inner product. These concepts expand the capabilities and versatility of vector algebra, allowing for more complex calculations and analysis in various fields.| Type of work | Dot Product Calculation |
|---|---|
| Constant force and displacement | Work = Force * Distance * cos(θ) |
| Variable force and displacement | Work = ∫ F * ds |
Finding Projections using Dot Product
The dot product is a fundamental concept in vector algebra that allows for the calculation of the projection of one vector onto another. By using the dot product, one can determine the component of a vector that lies in the direction of another vector. To find the projection of vector A onto vector B, one can use the formula: **Projection of A onto B = (A dot B) / \ |B| ² * B** This formula involves taking the dot product of vectors A and B, dividing it by the magnitude of vector B squared, and then multiplying it by vector B. The resulting vector represents the projection of vector A onto vector B. This concept is commonly used in various fields such as physics, engineering, and computer science, where understanding the direction and magnitude of vectors is crucial for solving real-world problems. Finding projections using the dot product offers practical applications in areas such as:- Physics: Calculating the component of a force acting on an object in a certain direction.
- Engineering: Determining the displacement of an object along a particular axis.
- Computer science: Utilizing vector transformations in computer graphics or simulations.
Solving Problems Involving Forces and Displacements
The dot product plays a crucial role in understanding the geometric properties of vectors and is particularly useful in solving problems related to forces and displacements. By calculating the dot product, one can determine the angle between two vectors, find the length or magnitude of a vector, calculate the projection of one vector onto another, and even determine if two vectors are orthogonal. In the field of physics, engineers and scientists frequently use the dot product to analyze forces acting on objects and calculate displacements. By decomposing forces into their components and taking dot products, they can determine the work done by a force on an object and calculate the energy transfer. This enables them to understand the behavior of objects under different forces and make predictions about their motion. In engineering applications, the dot product is utilized to analyze mechanical systems by calculating the work done by forces on different parts. It is also essential for understanding electricity and magnetism, as it allows engineers to calculate the dot product between electric fields and magnetic fields to determine the amount of force or torque exerted. While the dot product is a powerful tool in solving problems involving forces and displacements, there can be challenges when dealing with large datasets or complex calculations. However, advancements in computational power and algorithms are continuously improving the efficiency and accuracy of these calculations. Looking ahead, the dot product is poised to play a significant role in future developments in fields like robotics, autonomous systems, and advanced materials. As technology progresses, the ability to accurately calculate and analyze forces and displacements using the dot product will become even more critical for solving real-world problems and advancing these fields. The dot product is a fundamental concept in vector algebra that has practical applications in solving problems related to forces and displacements. Its versatility and capabilities make it an invaluable tool in fields such as physics, engineering, and computer science.Comparison of Dot Product with Other Concepts
| Concept | Definition | Application |
|---|---|---|
| Dot Product | Calculates the scalar product of two vectors | Determining angles, lengths, projections, and orthogonality |
| Cross Product | Calculates the vector product of two vectors | Finding the vector perpendicular to two given vectors |
| Inner Product | Generalization of dot product for abstract vector spaces | Defining lengths and angles in more advanced mathematical contexts |
- [Math Is Fun – Dot Product](https://www.mathsisfun.com/algebra/vectors


Leave a Reply